 |
|
МЕНЮФестивали и конкурсы Семинары Издания О МОДНТ Приглашения Поздравляем НАУЧНЫЕ РАБОТЫ |
Реферат: Экономико-статистический анализРеферат: Экономико-статистический анализI. Введение. Экономико-статистический анализ, прогнозирование и его значение. Методы составления прогнозов курсов валют. II. Построение трендовой модели. 1) О трендовой модели. 2) Выбор математической функции. Расчет и анализ темпов роста курса доллара. 3) Расчет линейной и квадратичной модели на основе метода наименьших квадратов. 4)Расчет и оценка ср. квадратичного отклонения. 5) Вывод о несответствии моделей. III. Экономический анализ. 1) Зависимомть между темпами роста инфляции и темпами роста курса доллара. Построение уравнения регресси на основе этой зависимости. 2) Анализ зависимости между динамикой роста курса доллара и разницей между спросом и предложением. 3) Анализ зависимости между ростом курса доллара брутто-оборотом торгов на ММВБ. 4) Вывод о переходе динамики роста курса доллара на новый уровень. и определение примерной даты перехода. IV. Построение трендовой модели с учетом перехода темпов роста курса на новый уровень. 1) Построение нового тренда. 2) Расчет среднеквадратичного отклонения и ошибки тренда в %. 3) Прогнозирование валютного курса с применением трендовой и регрессионной моделей. V. Общие выводы о полученном тренде. I.Введение. Построение экономических моделей и их дальнейшее практическое применение в наше время приобретает большое значение. Грамотно построенная модель позволяет предвидеть и проконтролировать ту или иную экономическую ситуацию основываясь не на интуиции, а на достоверном анализе уже имеющихся данных. Во всех современных производственных и коммерческих фирмах, а также в банках важнейшим звеном в структуре управления является аналитический отдел. Задача такого отдела - разработка вариантов перспективного развития предприятия. Подобного рода планирование и прогноз осуществляется при помощи различных математических моделей. Такие модели заложены в основу компьютерного програмного обеспечения (типа “Statgraph”, “Статистика” и т.п.). Курс рубля по отношению к американскому доллару является в нашей стране основным индикатором экономического положения (не беря в расчет последние пять месяцев, когда курс доллара силами ЦБ не выходит за рамки введенного в июле валютного корридора). Поэтому проводятся всевозможные попытки выявить динамику роста курса доллара и напрямую связать ее с уровнем инфляции в стране, ситуацией на валютной бирже и т.п. . А на основе полученных моделей делается прогноз. Целями такого прогнозирования является стремление компаний и банков повысить эффективность принимаемых решений, улучшить страхование валютных рисков. Также прогнозные оценки используются профессиональными финансовыми спекуляторами (валютными диллерами, брокерскими конторами), играющими на разнице курсов валют, ставок процента, курсов ценных бумаг на рынках различных стран и в различные интервалы времени. Можно выделить 5 основных методов прогнозирования плавающих курсов валют,применяемых в настоящее время. Первый подход базируется на теории эффективных валютных рынков, т.е. на модели равновесия в условиях совершенной конкуренции и концепции реальных ожиданий. В соответствии с ним на мировом валютном рынке присутствует множество продавцов и покупателей,вход на этот рынок относительно свободен и доступен,спрос и предложение гибко реагируют на изменение котировок, участниками рынка правильно учитывается вся доступная информация. Согласно этой концепции, невозможно сделать прогноз лучше рыночного. Второй метод прогнозирования основывается на анализе временных рядов динамики курса валюты. При этом применяются стандартные эконометрические процедуры - выделяется тренд в развитии курса, циклические колебания, сезонная компонента, после чего выравненные прошлые тенденции экстраполируются на будущий период. Среди практиков сейчас популярен “технический анализ” динамики курса. Базой этого метода также является выявление тренда. Однако главной задачей приэтом выступает правильное определение начала и конца тренда курса валюты. Такой подход не может рассматриваться как прогнозная модель в узком смысле слова, так ка здесь нет стремления установить уровень будущего курса - устанавливаются лишь время и направления изменения (поворотные точки) в тенденции развития котировок валюты. Одним из распространенных подходов к прогнозированию валютных курсов является “фундаментальный анализ”, в рамках которого курс определяется в зависимости от изменения “фундаментальных факторов” (соотношения темпов роста денежной массы, реальных доходов, ставок процента, товарных цен в сравниваемых странах). При этом прогноз будущей динамики курса является производным от правильности предварительных прогнозов соответствующих параметров (количества денег, ВНП, инфляции и т.п.) в сравниваемых странах. Наконец,”интуитивный”подход к прогнозированию валютных курсов. Поскольку динамика последних редко может быть обличена в строгую математическую форму или точно описана,то для ее прогнозирования применяется на практике такой метод,как свободная оценка специалистов,базирующаяся на опыте наблюдений за поведением рынка и участие в операциях на нем. Однако неправомерно и непродуктивно противопоставление различных из перечисленных подходов. Наоборот, применение одного метода прогнозирования не должно исключать возможности использования других. При этом технический анализ пригоден для краткосрочного, а фундаментальный - для средне- и долгосрочного. Из изложенных выше методик наиболее предпочтительным для простого неэкспертного анализа является построение трендовой модели с дальнейшим прогнозом. Данные для тренда берутся целиком за 1994 год. II.Построение трендовой модели 1) О трендовой модели. На практике наиболее распространенными методами статистического изучения тренда являются : укрупнение интервалов, сглаживание скользящей средней, аналитическое выравнивание. Применение в анализе рядов динамики первых двух методов позволяет выявить тренд для его описания, но получать обобщенную статистическую оценку тренда посредством этих методов невозможно. Решение этой более высокого порядка задачи - измерения тренда - достигается методом аналитического выравнивания . Основным содержанием метода аналитического выравнивания в рядах динамики является то, что основная тенденция развития Y рассчитывается как функция времени : Y = f(t) Определение теоретических (расчетных) уровней Y производится на основе так называемой адекватной математической функции ,которая наилучшим образом отображает основную тенденцию ряда динамики.Подбор адекватной функции осуществляется методом наименьших квадратов - минимальностью отклонений суммы квадратов между теоретическими Y и эмпирическими Y уровнями :
Значение уравнения (1) состоит в том, что при изучении тренда оно принимается в качестве критерия оценки соответствия расчетных (теоретических) уровней с фактическими (эмпирическими) уровнями ряда динамики. Важной проблемой при применении метода аналитического выравнивания, является подбор математической функции, по которой рассчитываются теоретические уровни тренда. От правильности решения этой проблемы зависят выводы о закономерностях тренда изучаемых явлений. Если выбранный тип математической функции адекватен основной тенденции развития изучаемого явления во времени, то синтезированная на этой основе трендовая модель может иметь полезное применение при прогнозировании и в других практических целях. 2)Выбор математической функции. Для правильного выбора математической функции, на основе которой будет синтезироваться трендовая модель пранализируем базисные темпы роста курса доллара по мясяцам за 1994 год. Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем (базисные показатели). Расчитаем базисные темпы роста курса доллара, характеризующие отношение двух уровней ряда и выражающиеся в виде коэффициентов. Темпы роста исчисляются делением сравниваемого уровня на уровень принятый за постоянную базу сравнения (в данном случае декабрь 1993г.):
Итоги расчетов помещены в таб. 1 После расчетов и анализа можно говорить об относительно ровном увеличениии темпов роста курса доллара (примерно на 0.06-0.11 ежемесячно), и только во втором полугодии намечается некоторое изменение. Теперь разница между двумя месячными показателями возрасла до 0.25-0.36. Такое соотношение темпов роста наиболее близко для линейной и квадратичной зависимости. Динамика курса доллара изображенная на рис. 1 также напоминает нечто среднеее между линейной функцией и парараболой. Для анализа динамики валютного курса за 1994 год и выявления общей тенденции его развития построим трендовую модель по двум математическим функциям : линейной и квадратичной. Временной интервал будет длинной в 5 дней (торговая неделя). 3)Расчет линейной и квадратичной модели на основе метода наименьших квадратов а)Линейная функция Y = bt + a (2) где a и b - параметры уравнения; t - обозначение времени. Параметр b является коэффициентом регрессии, определяющим направление развития. По методу наименьших квадратов находим a и b Дифференцируя выходим на следующую систему уравнений : Для решения этой системы обычно применяется способ определителей, позволяющий получать более точные результаты за счет сведения к минимуму ошибки из-за округлений в расчетах параметров: Применительно к анализируемым данным для определения алгоритмов (4.1) и (4.2) составляется матрица расчетных показателей (таб. 2) По итоговым данным таб. определяем по формуле (4.1) - а , по формуле (4.2) - b . По вычисленным параметрам производим синтезирование трендовой модели функции (см.формулу (2)) : Y=1171 + 39t б) Квадратичная функция. где a , b , с - параметры уравнения; t - обозначение времени. Параметр с характеризует постоянное изменение интенсивности развития (в единицу времени) ,а параметры a и b идентичны параметрам уравнения (2). Вычисляем параметры функции (5) на основе требований метода наименьших квадратов : Дифференцируя получаем следующую систему уравнений :
|
Приглашения09.12.2013 - 16.12.2013 Международный конкурс хореографического искусства в рамках Международного фестиваля искусств «РОЖДЕСТВЕНСКАЯ АНДОРРА»09.12.2013 - 16.12.2013 Международный конкурс хорового искусства в АНДОРРЕ «РОЖДЕСТВЕНСКАЯ АНДОРРА»
|
Copyright © 2012 г.
При использовании материалов - ссылка на сайт обязательна.

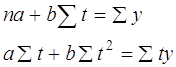 (4)
(4)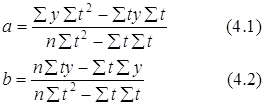
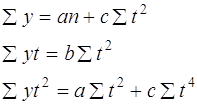 (5)
(5)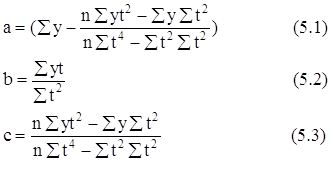
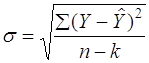 (
6 )
(
6 )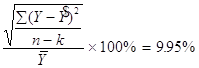
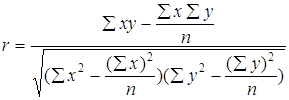
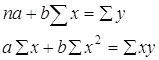 (11)
(11)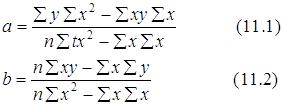
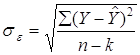 ;
;
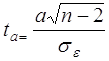 ;
;
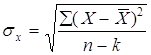 ;
;
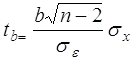 ;
;

